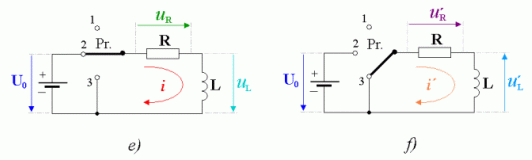
Všimnime si teraz, čo sa stane s obvodovými veličinami v obvode, keď prepneme prepínač Pr. z polohy 2) do polohy 3). Situácia je naznačená na obrázkoch e) a f). Obvodové veličiny doplníme v označení čiarkami - i´, uL´, uR´.
Ako z obrázka f) vidno, rezistor R je pripojený paralelne ku cievke L. Pokiaľ je ešte prepínača Pr. prepnutý v polohe 2) ( obráyok e)) a prebieha už ustálený stav, je v okolí cievky magnetické pole, ktoré je vytvorené prietokom prúdu i obvodom a jeho energia je daná vzťahom :
Hneď po prepnutí prepínača Pr. do polohy 3) sa prúd v obvode snaží zaniknúť. Proti tejto skutočnosti sa v cievke aktivuje proces, ktorý popisuje Lenzovo pravidlo a jednoducho ho môžeme interpretovať nasledovne :
Magnetické pole cievky, v okamihu skratovania cievky L rezistorom R, má tendenciu zaniknúť. Energia tohto poľa sa spotrebuje v cievke a to tým, že indukuje na svorkách cievky napätie uL´ takej orientácie, že smer prúdu i´ v obvode bude rovnaký ako smer prúdu i , ktorý toto magnetické pole v okolí cievky vytvoril. Z povedaného vyplýva a z obrázkov e) a f) je zrejmé, že napätie uL´ má opačnú orientáciu ako malo napätie uL v predchádzajúcom prípade, keď bol prepínač Pr. v polohe 2). ( Cievka L pôsobí ako zdroj energie pre obvod RL.)
Zánik magnetického poľa cievky je sprevádzaný poklesom napätia uL´ na nej ( je to proces podobný ako pri vybíjaní kondenzátora.) Poklesom napätia uL´ na cievke L klesá aj napätie uR´ na rezistore R ( rezistor R je paralelne ku cievke L ) a prúdu i´ v obvode. Rovnice popisujúce pokles jednotlivých obvodových veličín majú podobný tvar ako rovnice popisujúce pokles napätí a prúdu v obvode s rezistorom R a kondenzátorom C , ktorý sme analyzovali na začiatku tejto témy. Teda môžeme písať nasledujúce rovnice :
 |
(16) |
 |
(17) |
 |
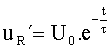(18) |
Znamienko v rovnici vyjadruje vzťah polarity obvodovej veličiny na obrázku f) k polarite obvodovej veličiny na obrázku e).
Grafické znázornenie rovníc (16), (17) a (18) sú časové priebehy, znázornené na nasledujúcich obrázkoch.
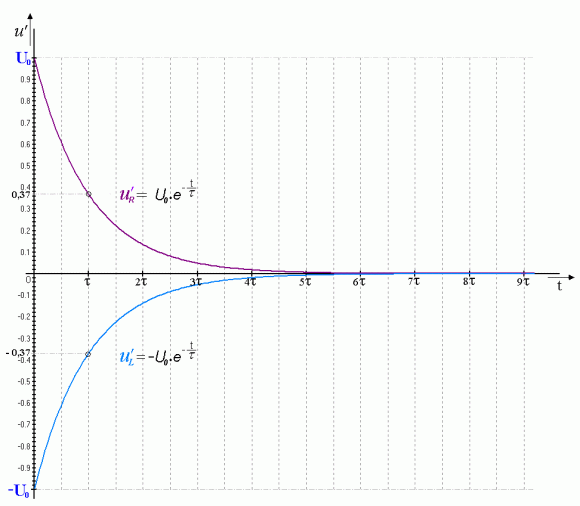
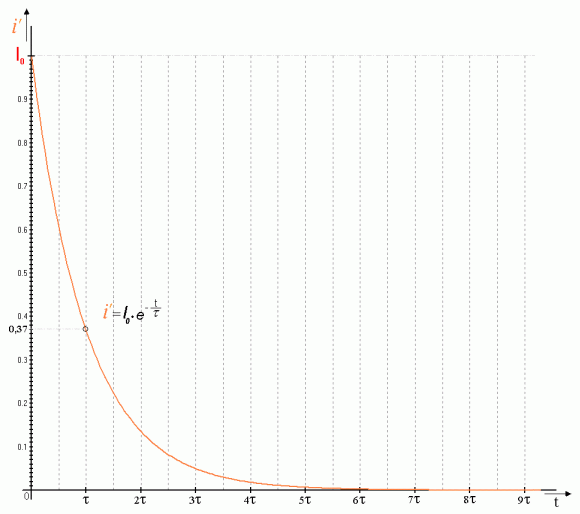
Ak teraz za čas t v rovniciach (17), (18) a (19) dosadíme časovú konštantu t , dostávame pre prúd i´ a napätia uR´ a uL´ hodnoty :
| prúd v obvode | - | i´(t) = I0.e-1 = 0,368.I0 |
| napätie na cievke L | - | uL´(t) = - U0.e-1) = - 0,368.U0 |
| napätie na rezistore R | - | uR´(t) = U0.e-1 = 0,368.U0 |
Po skončení prechodného deja zániku prúdu v RL obvode, pre čas t >> 5.t, môžeme písať pre napätia a prúd :
V záverečnej časti tejto témy, v ktorej sme analyzovali správanie sa obvodových veličín elektrického obvodu, napätia a prúdu, si urobme malú rekapituláciu a zapamätajme si :
Ak chceme v obvode s reaktančným prvkom popísať rovnicou nárast nejakej obvodovej veličiny od nulovej hodnoty po jej maximálnu hodnotu, v danej rovnici sa musí vyskytovať člen 
. Teda, ak máme nejakú obvodovú veličinu a s jej maximálnou hodnotou A0, potom jej nárast popíšeme rovnicou :
Ak zasa chceme popísať pokles obvodovej veličiny od jej maximálnej hodnoty po nulovú hodnotu, v danej rovnici sa musí vyskytovať člen 
. Teda, ak chceme popísať pokles obvodovej veličiny a , ktorá má maximálnu hodnotu A0, potom jej pokles popíšeme rovnicou :
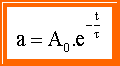
V úvode tejto témy sme si povedali, že prechodný dej vypĺňa časový interval medzi dvoma ustálenými stavmi obvodu a ako z vyššie uvedených vzťahov vyplýva, je charakterizovaný nelineárnou ( exponenciálnou ) závislosťou obvodových veličín ( v našom prípade prúdu a napätia ) na čase !!
Pre ilustráciu zmien exponenciálnych členov vyskytujúcich sa vo vzťahoch popisujúcich nárast a pokles obvodovej veličiny uveďme tabuľku ich hodnôt v závislosti od času t :
| t | 0 | t | 2.t | 3.t | 4.t | 5.t | 10.t | ¥ |
|
1 | 0,368 | 0,135 | 0,05 | 0,018 | 0,007 | 0,000045 | 0 |
|
0 | 0,632 | 0,865 | 0,95 | 0,982 | 0,993 | 0,999955 | 1 |